算数が伸びないわけ　算数を伸ばす勉強法

通過算とは、列車が橋やトンネルを通過するというタイプの問題だ。

 

通貨にかかる時間、列車の速度、列車の長さ、橋やトンネルの長さなど、様々な設問があるが、基本問題は比較的簡単だ。

 

基本問題のバリエーションとしては、

の2パターンがある。

 

これらは、1編成の列車が橋やトンネルを通過するというタイプの問題だ。

 

一方、応用問題として、2編成の列車が登場する通過算もある。

 

これは旅人算の応用でもある。

 

パターンとしては、

という2パターンがある。

 

通過算の解き方　後発の列車が先発の列車を追い抜く

通過算　列車の追い抜き問題　例題

 

考え方

答えは秒数で答えるので、速さを全て秒速に換算します。

 

時速を分速に換算するには60で割ります。

 

さらに分速を秒速に換算するには、60で割ります。

 

なので時速から秒速に換算するには、60*60で割れば良いという事になります。

各駅列車に乗っている人から見た急行列車の速度（相対速度）は、

になります。

 

さて、急行列車が各駅列車に追いついて、完全に追い抜くというのは、次の図のような状態を指します。

通過算　列車の追い抜きの図

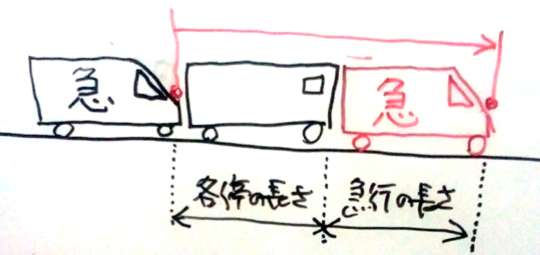
急行列車の先頭が各駅列車の最後尾に来たところから、急行列車の最後尾が各駅列車の先頭より前に来たところまでが、追い抜き状態です。

 

つまり、急行列車の長さ＋各駅列車の長さ　の距離を、急行列車が追い抜いていく秒数を答えることになります。

 

 

 

 

通過算の解き方　列車がすれ違う問題

通過算には、2編成の列車が、すれ違うタイプの問題もあります。

 

通過算　列車がすれ違うタイプの例題

考え方

一つ前の例題と速度が同じように、秒速に換算します。

で、「相対速度」（あるいは接近速度）が問題になりますが、向かい合わせなので、足し算になります。

各駅列車に乗っている人から見ると、急行列車は秒速40mの速度で向かってくるわけですね。

 

通過算の解き方　列車がすれ違う場合の図

 

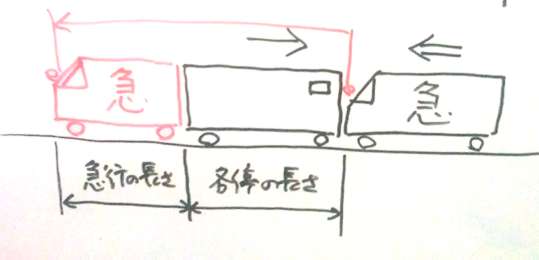
秒速40mで、二編成の車両分を駆け抜けていくので、答えはこうなります。

 

考え方としては、旅人算の出会うパターンと同じですね。