複雑な操作をする食塩水の問題
更新日:

食塩水の問題は、簡単な問題から複雑な問題まで、様々な問題が作れる。
まず単純に一つの食塩水の濃さや、溶けている食塩の量を求める問題。
これは、
全体量×濃さ=溶けている食塩の量
…という計算式だけで解ける。
次に2つ以上の食塩水を混ぜ合わせる「操作」がある問題。
濃さが異なるA液とB液があって、これを少しずつ混ぜ合わせる。
たとえば5%の食塩水と、10%の食塩水から、8%の食塩水を作ると言うような問題。
これは結構難しい。
普通は、中学2年生で習う連立方程式で解くが、中学受験では連立方程式は使えない。
なので代わりに「面積図」や「ツルカメ算」を使って解いたりする。
他にも水を加えたり、蒸発させたりという「操作」もある。
水を加えたり蒸発させると、全体量も変わるし、濃さも変わるから、意外に難しい問題になったりする。
水は濃度0%の食塩水と見なせば、他の食塩水同じように計算できる。
食塩水の問題は、何段階も操作を加えれば、いくらでも複雑な問題が作れる。
食塩水 混ぜ合わせの図
こういう複雑な操作をする食塩水の問題を解くには、図だとか表を使わないと解けない。
暗算なんかすると、どこで間違えているのかも分からなくなるし。
混ぜ合わせの図というのは、こんな感じで描く。
不明な部分は□を入れておき、タテヨコで計算できるところを計算していく。
計算のルールは次のようになる。
- 全体量は、全体量同士で計算する。
- 食塩の量は、食塩の量同士で計算する。
- 濃さはビーカーの中だけで計算する。
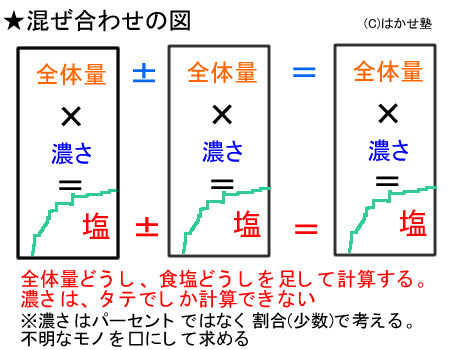
これは中学に上がってからも使えるから、ちゃんとこの通り描いてください。
A液とB液を、交互に混ぜ合わせていくような問題の場合は、2段にこれを描く。
横ではなく、タテに表を作る方法もある。
さっきの5%食塩水と10%食塩水を混ぜて8%食塩水を作る問題だと、こういう図になる。
| 5%食塩水 | 10%食塩水 | 8%食塩水 |
|---|---|---|
| ○g | △g | 100g |
| 0.05 | 0.1 | 0.08 |
| 8g |
足して100グラムの組み合わせになる組み合わせで、溶けている食塩の合計が8gになるようにすれば良い。
6年生の夏以降の家庭学習ミニ模試に
楽天ブックス(広告)
面積図を使った解法
この問題は、中学2年生なら連立方程式で解くが、中学受験の場合は面積図を使って解く。
縦軸に濃さをとり、横軸に食塩水の重さを取ると、面積が食塩の量になる。
食塩水の問題・面積図
合計の量が分かっているので、A液とB液を横並びで描く。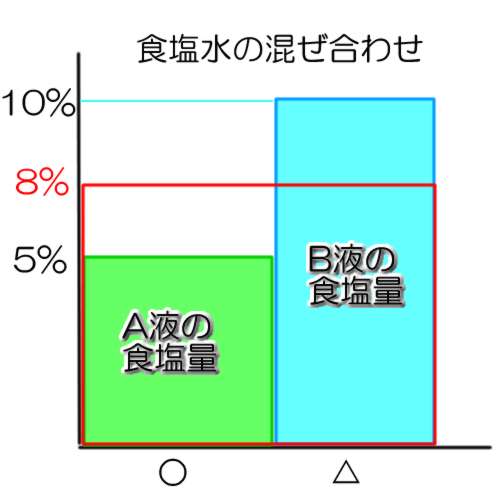
上の図で、B液が8%の赤い枠より上にはみ出た部分が、A液の足りない部分にちょうど収まれば、8%の食塩水が出来ることになる。
なので、 (8-5) * ○ = (10-8) * △ と言う関係になる。
これより、○:△=2:3 が分かるので、5%が40グラム、10%が60グラムになる。
この値を図に書き込めば、合っているかどうかが分かる。
こんな感じ。
| 5%食塩水 | 10%食塩水 | 8%食塩水 |
|---|---|---|
| 40g | 60g | 100g |
| 0.05 | 0.1 | 0.08 |
| 2g | 6g | 8g |
ツルカメ算による解法
あるいは、ツルカメ算で解いても良い。
100g全部を10%食塩水にすると、そこに含まれる食塩は10gだ。
10%食塩水を1グラムを、5%食塩水に置き換えると、食塩の量は、0.1-0.05=0.05グラム減る。
なので含まれる食塩の量を8グラムに減らすには、
(10-8)÷0.05=40
で、10%食塩水を40グラム減らして、5%食塩水を40グラム増やせば良い。
これにより、同じ答えになる。














