面積図でなくても解ける
更新日：
中学受験の面積図の話の続き。
A君は、１００円のノートを、何冊か買いました。
B君は、８０円のノートを、何冊か買いました。
A君が買った冊数は、B君より５冊少なかったです。
また代金も、１６０円少なかったです。
さて、A君は、何冊ノートを買ったでしょう？
この例題では、ノートの価格×冊数＝代金 という掛け算が出来る。
なので、縦軸にノートの価格、横軸にノートの冊数を取ると、できた長方形の面積はノートの代金を表す。
問題では、冊数の差とノートの代金の差が与えられているので、A君の図とB君の図を重ね合わせて描き、はみ出た部分を考えれば良い。
面積図の例
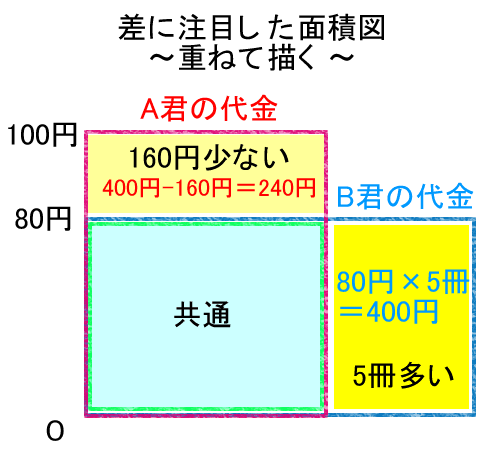
薄緑色の部分は共通なので、ここは無視して、はみ出ている部分を比べる。
B君はA君より5冊多いので、右側に5冊分ほどはみ出している。
このはみ出し部分の面積は、B君のノート代金の一部ってことだ。
B君の買ったノートの価格は80円なので、この部分は８０円×５冊で４００円になる。
ここで、A君の支払ったノート代金は、B君より160円少ないので、上にはみ出した部分は、
400円 － 160円 ＝ 240円
A君のはみ出し部分は、タテが20円分で、ヨコが冊数だから、
240円 ÷ 20円 ＝ 12冊
となって、A君の買ったノートが１２冊というのが分かる。
これが面積図を使った解法になる。
ツルカメ算による解法
「もし二人とも、同じ冊数ノートを買ったらどうなる？」と考えるのが、ツルカメ算による解法だ。
これは生徒が、仮定で物事を考える事ができることが前提だ。
残念ながら、仮の話を考えられないタイプの子供さんも居るし。
それはさておくとして、ツルカメ算を進めよう。
まずA君はB君より5冊少ないわけだから、5冊増やして同数にしてみる。
A君が5冊ノートを追加で買うと考えると、A君の代金は500円増える。
元々、A君の代金は160円少なかったので、A君が5冊追加した結果、B君より500円－160円＝340円ほどノート代金が多くなる。
A君の買ったノートは、B君のノートより1冊当たり20円高いので、そこから次の式が立てられる。
20円×□冊＝340円
これを解けば、340円÷20円＝17（冊）という数が出てくるね。
ただし実際にA君が買ったのは、これより５冊少ないので、１２冊買ったと分かるわけだ。
こういう風に、面積図やツルカメ算を使うのが、中学受験の算数の特殊な部分になる。
そしてどちらも子供にとって理解しがたい部分があるので、そう簡単には身につかない。
