分配算 和差算、倍数算、相当算
更新日：
分配算とは、モノやお金をいくつかに分ける問題だ。
分配算には3つのタイプの問題形式があって、別の名前が付いていることも多い。
- 和差算 … 合計と差が与えられて分けるタイプ
- 倍数算 … 2倍とか3倍といったヒントが与えられているタイプ
- 相当算 … 小数や分数で割合が与えられているタイプ
和差算
和差算 例題
8メートルのリボンを、窓の周りに飾るため、4本に切ろうと思います。
4本のうち2本は、窓の左右にタテに飾ります。
残りの2本は、窓の上下にヨコに飾ります。
窓のタテの寸法を測ったところ、ヨコの寸法より、60cm短くなっていました。
またリボンはちょうどで、あまりはありませんでした。
さて、タテのリボンとヨコのリボンの長さは、それぞれ何cmですか。
考え方
まず、タテのリボン2本は長さが同じです。
ヨコのリボン2本も長さが同じです。
リボンにあまりが出ないので、8メートルのリボンをまず半分に切り分けます。
半分に切り分けた4メートルのリボンから、タテのリボンとヨコのリボンを作ります。
タテの寸法がヨコの寸法より60cm短いということは、ヨコの寸法がタテの寸法より60cm長いと言うことです。
和差算 線分図を使った解法
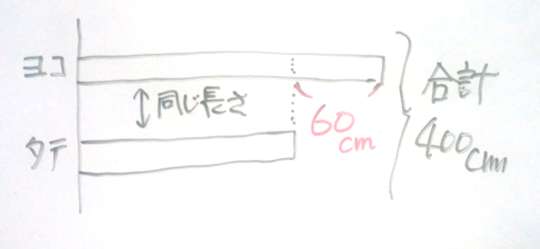
ということで、まず4メートルのリボンから60cmのところに印をつけておきます。
60cm分のリボンを除くと、あとは同じ長さになるわけですので、
(400cm - 60cm )÷2＝170cm
となり、これがタテのリボンの寸法ですね。
ヨコのリボンは、これよりも60cm長いので、
170cm + 60cm = 230cm
と言う風に計算できます。
和差算では、差の分を除くと同じになることを利用して解くわけですね。
分配算 倍数算タイプ
2倍とか3倍といったヒントが与えられているタイプで、比で与えられていることも多い問題です。
和差算よりも抽象度が高くて、難しい問題になります。
A君とB君は、二人で近くの動物園に遊びに行きました。
動物園に行く途中で、持ってきたお小遣いを比べてみると、A君とB君のお小遣いの比は、２：１でした。
動物園の入り口で、入園料500円をそれぞれ払った後、残ったお小遣いを比べてみると、３：１になっていました。
A君とB君が動物園に入る前に持っていたお小遣いは、それぞれいくらだったでしょうか。
倍数算を線分図で解く その１
倍数算は、線分図を描かないと、関係が見えないので、まず書いてみます。
最初の比を○印で囲み、後の比を△印で囲んで区別します。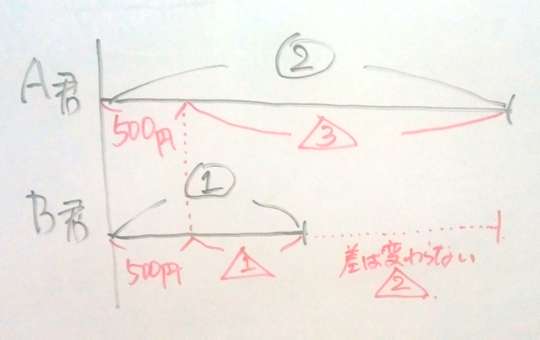
注目するのは、「入園料を払う前と後で変わらない部分」の長さです。
この問題の場合、どちらも同じ入園料を支払うので、持っているお小遣いの差は変わりません。
上の図で見ると、○印の１と△印の２が等しいことが分かります。
倍数算を線分図で解く その２
○１＝△２になっていると分かったので、○印を△印に換算して置き換えて見ます。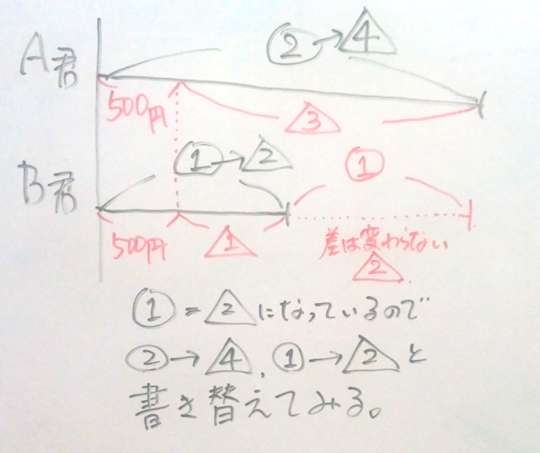
ここで入園料の500円が、△印何個分になるのか考えると、図から△１=500円だと分かります。
A君のお小遣いは、△4個分なので、500円×4＝2000円。
B君のお小遣いは、△2個分なので、500円×2＝1000円となりますね。
このタイプの問題は、線分図が描けないと、恐らく解けないと思います。
