植木算は、公式より図示
更新日：
植木算とは、決められた場所に木を植えるタイプの問題だ。
問題のタイプとしては
- 直線状に木を植える問題
- 円周状に木を植える問題
- より複雑な植え方をする問題
に分かれる。
植木算を解く際に重要なのは、「問題を、図示できること」だ。
問題の状況を図示できなければ、植木算の公式など覚えても役には立たない。
算数が苦手な子供に、たくさん公式を覚えさせると、混乱して結局出来ないままになることが殆どだ。
中学受験の算数では、問題を図示できるかどうかが大きな鍵で、公式を覚えるのは二の次だ。
植木算の問題
植木算 例題
新しく出来た小学校は、海のそばにあって、まだ建設中です。
【問1】
海風が強いため、校庭の海側に木を植えることにしました。
海側の50メートルに2メートルおきに、等間隔に木を植える場合、木は最低何本必要ですか。
ただし両端には木を植えないモノとします。
【問2】
この小学校には、30メートル×20メートルの小さなプール設備も作ります。
このプール設備の周りに、2メートル間隔で等間隔で木を植える場合、木は何本必要ですか。
ただし、プール設備の四隅にも木を植えることとします。
植木算 考え方
問1の考え方
まず、問題を図示します。
左端をA地点、右端をB地点とします。
植木算の図その１
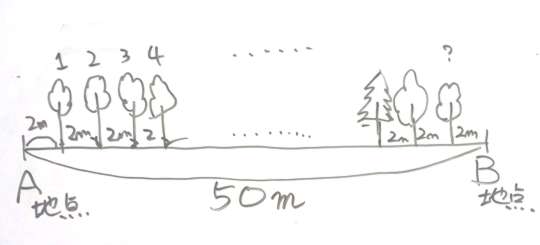
50メートルの校庭に、2メートル間隔で木を植えるので、2メートルずつに区切ります。
50m÷2m＝25 （区間）
区間の右端に1本ずつ木を植えていくと、25区間なので、木が25本必要になります。
ただ両端には木を植えないので、一番右端の区間には木が必要無いので、1本減らします。
25本-1本＝24本 …（答え）
問2の考え方
まず、20メートル×30メートルの長方形の図を描きます。
左上から、ABCDと言う風に記号をつけます。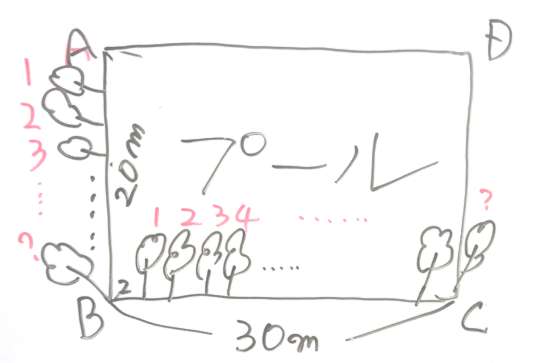
この図のA点からB点までの距離は20メートルですので、2メートルずつ区切ると10区間になります。
区間の終わりに木を一本植えるとすると、10本になりますね。
同様にB点からC点までの距離の30メートルを、2メートルずつ区切ると15区間になります。
よって、木は15本必要になります。
同様にC点からD点では10本、D点からA点までは15本の木が必要です。
ということで、
１０＋１５＋１０＋１５＝５０（本）
ですね。
図示したとおり、プール設備の四隅には木が植わっていますので、これが答えになります。
（因みに、四隅に木を植えないのであれば、ここから4本減らします）。
