仕事算は、表を使って解く方が分かりやすい
更新日:

仕事算は全体の仕事量を1と置くよりも、公倍数を使った方が、後々の計算が楽になる。
もちろんこれは「便法」であり、子供から「なぜ?」と尋ねられても、明確に応える事はできない。
説明の仕方とすれば、全体の仕事量を「1」、すなわち100%に決める方が、子供にとって分かりやすいハズだ。
ただ算数や数学というのは「あとあと計算しやすいから」「この方が便利だから」という理由で、定義が作られていることも多い。
なので「こういう風に決める方が、計算しやすくなるんだ。内緒だよ」という答え方で良いと思う。
ということで、今回も仕事算の話のつづきだ。
仕事算 例題4
A君は、ある仕事を完成させるのに10日かかります。
B君は、同じ仕事を完成させるのに9日かかります。
C君は、同じ仕事を完成させるのに8日かかります。
A君がこの仕事を出来るのは、月曜日と火曜日と水曜日と木曜日です。
B君がこの仕事を出来るのは、火曜日と水曜日と金曜日です。
C君がこの仕事を出来るのは、水曜日と木曜日と金曜日です。
(1)月曜日にこの仕事を始めたとすると、何曜日に完成しますか?
(2)何曜日に始めると、一番日数が少なくて済みますか?
この問題で、A君B君C君の1日あたりの作業量を整数で表すには、10と9と8の公倍数720を全体量にすれば良い。
720は最小公倍数ではないが、計算しやすければ別に問題は無い。
全作業量を720に決めれば、それぞれの一日あたりの作業量(人日:にんにち)は、次のようになる。
- A君の人日 … 72 (9×8)
- B君の人日 … 80 (10×8)
- C君の人日 … 90 (10×9)
ここまでは、例題3と同じだ。
6年生の夏以降の家庭学習ミニ模試に
楽天ブックス(広告)
曜日ごとの表を作ってみる
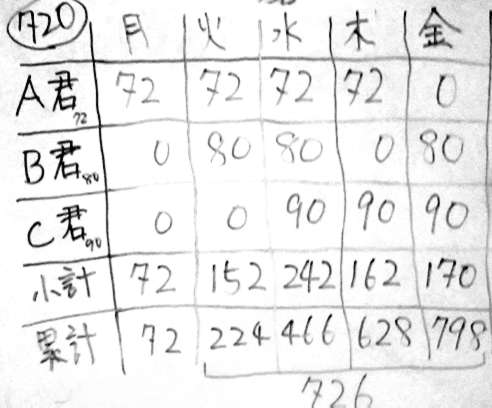
この表で考えると、月曜日から始めた場合、金曜日に仕事の全体量の720を越えることが分かる。
ということで、問1の答えは「金曜日」ってことだね。
そして問2も、この表を見て考える。
月曜日はA君しか仕事が出来ないので、月曜日を外して考えたい。
で、火曜日から金曜日までの工数を足すと(あるいは、金曜日の累計から月曜日の小計を引くと)、720を越える。
つまり火曜日から始めると金曜日に終わって、日数は4日になる。
他の曜日から始めると、必ず月曜日が含まれて、日数が5日になるので、4日以内にはならない。
ということで、問2の答えは「火曜日」ということになる。














