通過算 列車がトンネルや橋を通過する問題。
更新日:

通過算(つうかざん)とは、列車がトンネルや橋を通過する時間などを考える問題だ。
これは公務員試験やSPI適性試験などでも出題される問題で、要領が分からないと難しい。
中学受験で出題されるのは、トンネルや橋を渡る問題が殆どだが、適性試験では、列車同士がすれ違う時間なども問われたりする。
通過算で重要なのは、「どこから(起点)」「どこまで(終点)」をハッキリ捉えられているかと言う部分になる。
「トンネルに入った」ところから、「トンネルから出た」ところまでを、ハッキリイメージできるかどうかが、分岐点だ。
そのために絵や図を描くことが必要になってくる。
通過算 橋を通過する問題
トンネルや橋を通過する場合、列車の先頭がトンネルや橋にさしかかったところが「起点」になる。
一方、列車の最後尾がトンネルや橋を抜けたところが「終点」になる。
そのため、列車の長さを計算に入れないといけないのだが、これが小学生には難しいようだ。
通過算 例題1
950メートルの長さの鉄橋があります。
この鉄橋を電車が渡り始め、渡り終わるまでに1分間かかりました。
電車の時速が60kmだったとすると、電車の長さは何メートルですか?
通過算の図
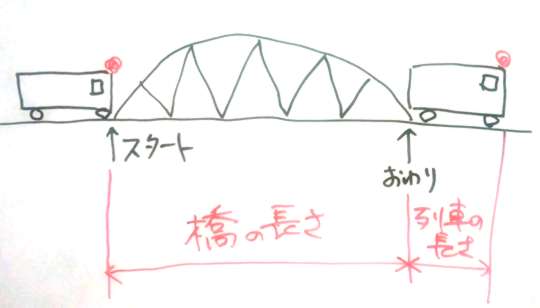
列車の先頭のヘッドランプをイメージする。
ヘッドランプが動いた距離が、列車が進んだ距離になる。
橋を渡りきる場合は、橋の長さと列車の長さの合計に相当する。
考え方
時速60kmで走っている列車が1分かかって渡りきったわけなので、進んだ距離は
60km×(1/60)=1km =1,000m
橋の長さが950mなので、列車の長さは50m。 … (答え)
6年生の夏以降の家庭学習ミニ模試に
楽天ブックス(広告)
通過算 トンネルに入っている時間
「トンネルに隠れている時間」を尋ねられる問題もある。
通過算 例題2
あるトンネルに列車が入って見えなくなってから、反対側の出口に列車の先頭が出るまで、3分かかります。
この列車が時速60kmで走っていたとすると、トンネルの長さは何メートルになりますか。
列車の長さは50mとします。
考え方
時速60kmの速さで3分かかっているので、進んだ距離は
60km × (3/60) = 3km
ここで考えないといけないのが、列車の長さになる。
ということで、トンネルに入っている図を描くと、次のようになる。
通過算 トンネルに入っている図
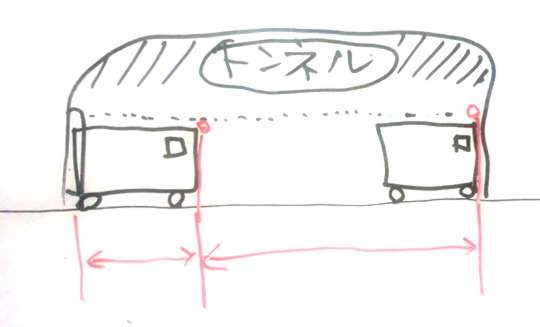
トンネルに列車が隠れると言うことは、列車の最後尾がトンネルに入った時点から、先頭がトンネルから出てくるところまでの間を意味する。
なので、3分で進んだ3Kmの距離は、トンネルの長さから列車の長さを引いたものと言うことになる。
ということで、トンネルの長さは、
3Km+50m=3,050m … 答え
と言うことになりますね。














