面積は概念？それとも具体的？
更新日：
面積がわからない生徒も、たまにいる。
面積というのは、具体的なようで、実は抽象的なものらしい。
たとえば、長さというのは、直感的に理解できるだ。
というのも長さが違うモノが二つあれば、並べてみると、どちらが長いか見れば分かる。
ところが面積ともなると、どちらの面積が大きいのかは、直感的に分からない。
体積ともなると、さらに抽象的だ。
面積や体積は、抽象概念
たとえば次のような、縦長の背の高いコップに入ったジュースと、太めのコップに入ったジュース。
どちらが多いかを幼児に尋ねるという実験がある。
形の異なる二つのコップに入ったジュース
実験に使ったジュースの分量は、どちらのコップに入っているのも同じにしてあるのだが、幼児の8割くらいは背の高いコップの方を指すという。
そして、なぜそちらを選んだかを問うと、ジュースの液面が高いからだと思うらしい。
幼児の場合、体積という概念を持っていないので、直感的にわかる高さ（長さ）で比較したわけだ。
一方、背の低い方のコップを選んだ幼児は、横幅の大きさを比べて選んだらしい。
どちらにせよ、ジュースの量を比べるために、長さで考えているわけだ。
面積や体積の考え方
幼児の実験で分かるように、長さを比べることは直感的に出来る。
しかし面積や体積というのは、直感的に比べることが出来ない。
そのため、面積や体積が理解できない子供も多い。
ただ面積なんて、ものすごく簡単な考え方だ。
１センチ四方の正方形が、ちょうど３個入れば、３平方センチメートル。
１メートル四方の正方形が、５個分なら５平方メートル。
考え方としては、これだけに過ぎない。
面積の概念とは
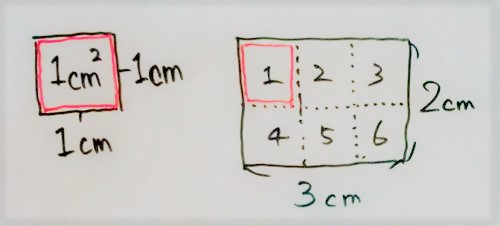
ところがこの考え方では、長方形の面積なら、まだ何となく分かるが、三角形だとか円の面積になると、途端に分からなくなる。
長方形なら、まだ1センチ角のマス目を数えることが出来るが、三角形や平行四辺形や台形の面積となると、お手上げだからだ。
具体的に一マス一マス数えられるところから、急に「面積の計算公式」に飛躍する。
そのため、小学校4年生や5年生あたりから、算数の授業について行けなくなる。
公式を使うのも計算手順の一つだと思って練習する子供と、公式を使う意味が分からず、拒否反応を示して覚えない子供に分かれてしまうわけだ。
これを克服するのは、結局、計算練習だと諭して、練習させるしかない。
だって面積の公式なんて、単にマス目を数えるのが面倒だから作られたモノであって、特に意味なんか無いんだもん。
中学3年生になると、ルート（平方根）の計算で嫌になる女の子も多いが、こういうのは単なる計算で、特に理解すべきモノでもなんでも無い。
ただ、計算できるように、練習を繰り返せば良いだけなのだ。
