面積図やツルカメ算が難しい理由
更新日：
面積図やツルカメ算は、難しい。
というのも、どちらも具体的ではなく、抽象的なモノだからだ。
子供にとって、目に見えたり触ったり出来る具体的なモノは、理解しやすい。
しかし形がないものや、仮定の話は、抽象的で理解しにくい。
面積図など、よくよく考えたら、おかしい。
というのも面積図では、面積が長さを表したり、面積が食塩量を表したり、面積が代金を表したりする。
普通の子供にとって、面積は面積で、長さは長さだ。
なので面積が長さを表したり、重さを表したり、代金を表すというのは、理解しがたい。
面積と長さは「違うもの」であり、単位も違うわけだし。
面積図の仕組み
面積図では、掛け算で求めることが出来るモノは、面積（の大きさ）で表すことができる。
- 速さ ＊ 時間 ＝ 進んだ距離
- 濃さ ＊ 食塩水の重さ ＝ 溶けている食塩の重さ
- りんご1個の値段 ＊ 個数 ＝ 代金
と言うような関係があった場合、イコールの右側にあるモノは、面積で表せる。
食塩水の問題・面積図
縦軸を濃さ、横軸を食塩水の重さにすると、長方形の面積が食塩の量を表す。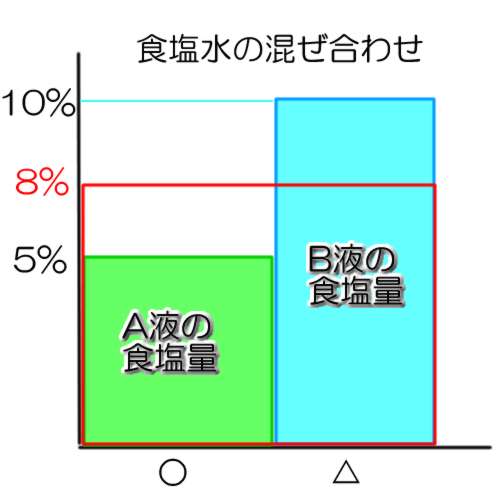
仮定の話を考えることが出来ない子供もいる
ツルカメ算だって、抽象的な考え方だ。
例えば、次のような例題があったとしよう。
例題
A君が1個200円のリンゴと、1個50円のミカンを、合わせて10個買ったとき、代金が1,100円でした。
A君は、リンゴとミカン、それぞれいくつ買いましたか？
この問題は、そもそもナンセンスな問題で、リンゴとミカンをいくつ買ったかは、A君に尋ねれば良い。
なので少し問題を替えてみる。
例題・改
1個200円のリンゴと、1個50円のミカンが売られています。
みんなに分けるのに、合計10個必要ですが、予算は1,100円しかありません。
A君は、リンゴが好きなので、リンゴを出来るだけ多く買いたいのですが、それぞれいくつ買えば良いでしょう？
この問題をツルカメ算で解く場合、まずリンゴかミカン、どちらかだけ買う事を考える。
A君はリンゴが好きなので、まずリンゴを10個全部買うことにする。
リンゴ10個の代金は2,000円になるので、900円足りない。
そこでリンゴを1個あきらめて、ミカン1個買うことにする。
そうすると、必要な代金は、 200円 － 50円 ＝ 150円 だけ減る。
同じ事を繰り返して、代金を900円減らすとすると、
900円 ÷ 150円 ＝ 6 （回）
となるので、リンゴ6個を、ミカン6個と交換すれば良い。
よって、A君が買うのは、
A. リンゴ4個とミカン6個
になる。
これがツルカメ算を使った解法だ。
ここで問題になるのが、「10個リンゴを全部買うとすると」と仮定することだ。
実際は、リンゴ10個買わないわけだから、これは抽象的な事になる。
そこで紙にリンゴとミカンの絵を描いて、理解させようとするのだが、理解できない子供も多い。
「仮の話」が出来ないタイプの子供もいるのだ。
ましてやこれが食塩水の問題になると、抽象的すぎて、頭の中がモヤモヤしてキレれたりすることもある。
